흥미로운 IT

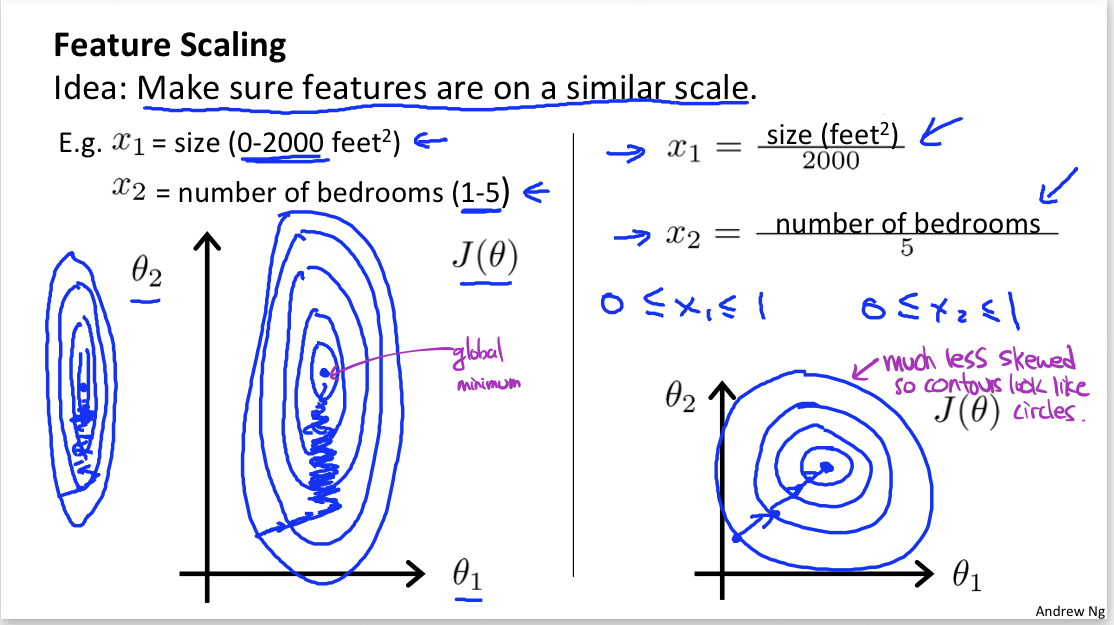
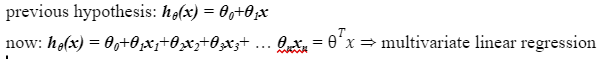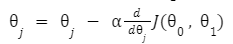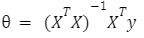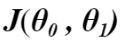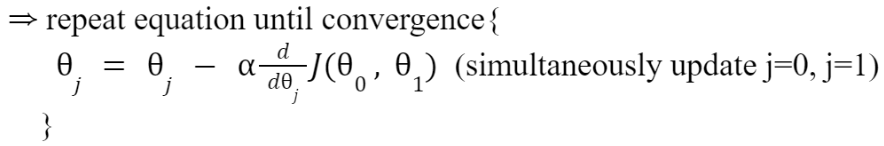Classification: y = 0 or y = 1

if hθ(x) ≥ 0.5, predict y=1

if hθ(x) < 0.5, predict y=0

⇒ logistic regression: 0 ≤ hθ(x) ≤ 1

Hypothesis Representation

- Sigmoid function (==logistic function)

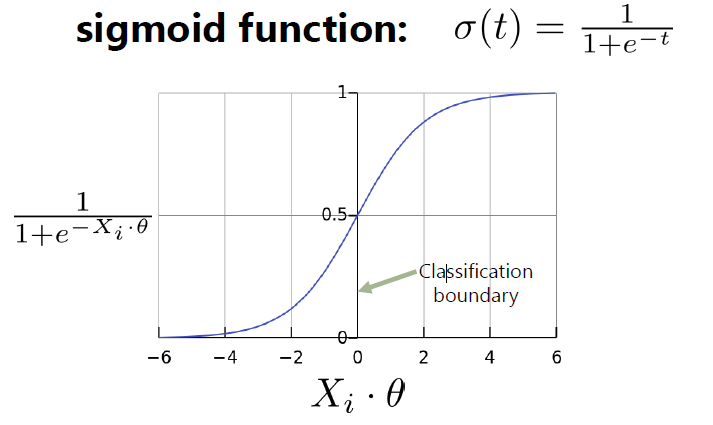
(cf) hθ(x) = 0.7 ⇒ 70% chance of ~~~

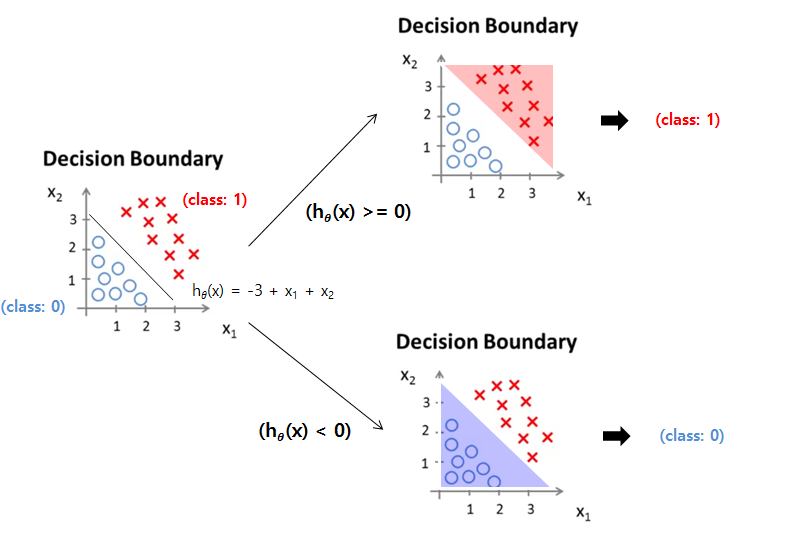
Decision boundary

hθ(x) = g(θ0+θ1x1+θ2x2)  ⇒  predict y=1 if -3+x1+x2 ≥ 0

Cost function

- How to choose parameter θ? 

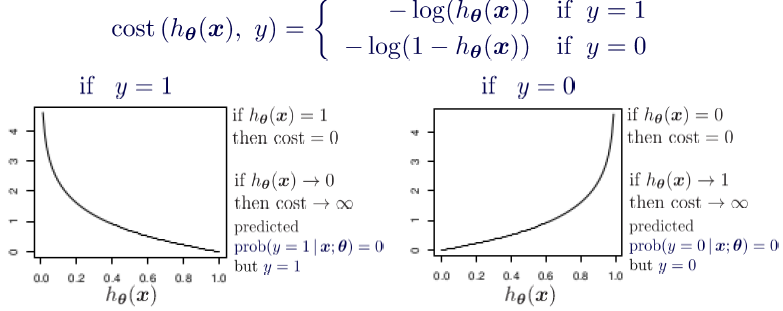
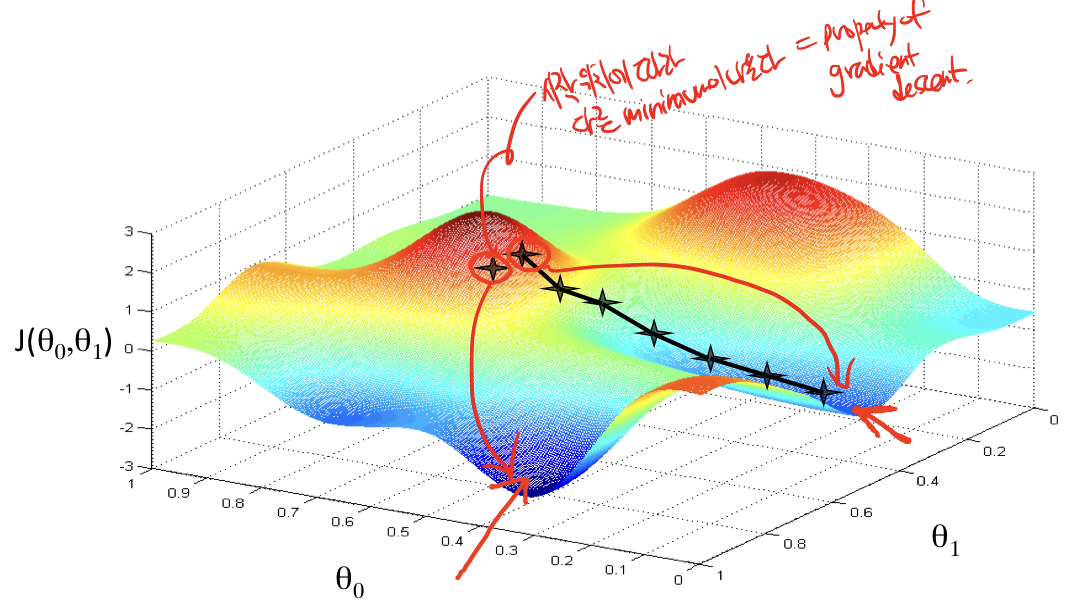
Simplified cost function and gradient descent

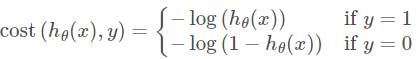
* convert the two lines into one line

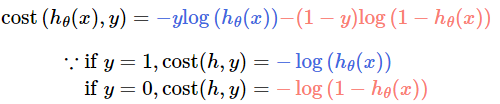
Logistic regression cost function

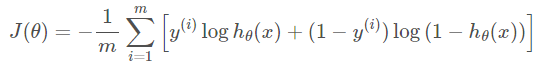
Gradient Descent

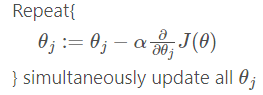
 *Looks same as linear regression!

BUT, hθ(x) are different! ==>

Multi-class classification (one-vs-all)

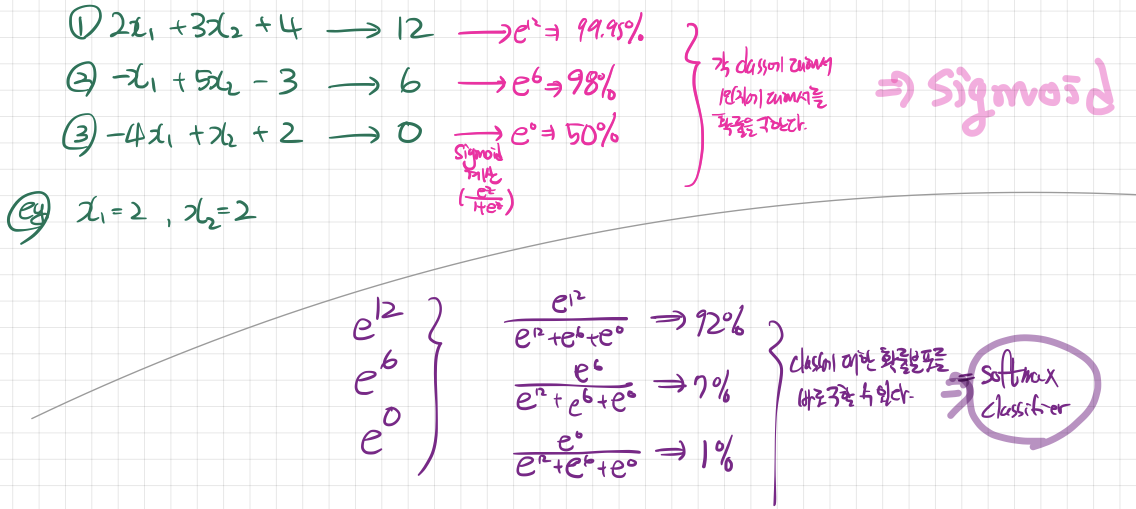
Sigmoid function  VS  softmax classifier

⇒ sigmoid: get percentage on how y might equal to 1 for each class

⇒ softmax: get the distribution of percentage of the classes

2022.01.25

Coursera - Machine Learning_Andrew Ng - Week 2

Multiple features(variables)

Gradient descent for multiple variables

Gradient descent in practice 1: Feature Scaling

- feature scaling

: simple trick to apply → make gradients run much faster and converge in a lot fewer other iterations.

: make sure features are on a similar scale ⇒ get every features into approximately a -1<=xi<=1 range

- mean normalization

Gradient Descent in practice 2: Learning rate

- Debugging: make sure gradient descent is working correctly

        (use visualization using plot vs automatic convergence test)

If α is too small ⇒ slow convergence

If α is too big ⇒ J(θ) may not decrease on every iteration; may not converge

Features and Polynomial Regression

Normal Equation formula

⇒ Compare with Gradient Descent

Gradient Descent	Normal Equation
needs to choose α	no need to choose α
needs many iterations	don't need iteratation
works well even when n is large	slow if n is very large + need to compute

Supervised learning

-classification vs regression(contiguous variables)

Unsupervised learning

-no answers given to the algorithm ⇒ computer automatically analyze

-cocktail party problem ⇒ 2 audio recordings → separate out the two voices ⇒ can be done with single line of code

⇒ [W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x’);

⇒ use “Octave” or “Matlab” ⇒ it’s faster

[Linear Regression]

Model Representation

-supervised learning has training set

-training set → learning algorithm

* hypothesis:

Cost Function

⇒ Goal: minimize J(θ0 , θ1) ⇒ global minimum

⇒ use contour plots/figures for visualization

⇒ linear line of h(x) is converted to a single point in cost function graph

Gradient Descent Algorithm

If is α too small ⇒ gradient descent can be slow (alpha = step size)

If is α too big ⇒ gradient descent fail to converge, or even diverge

α rate doesn’t need to decrease →automatically take smaller steps

Batch Gradient Descent: every step needs to calculate all training sets in batches

Review:

Although there is difficulty in understanding the whole process, particularly the gradient descent equation, I am fairly able to get the big picture and the important concepts of machine learning regarding supervised/unsupervised learning, model representation, cost function, and gradient descent algorithm.

I am currently able to follow the contents and able to solve the quiz in Coursera for each lecture without much difficulty, yet!